Analysis of Uniform Phased Arrays (2)
In the previous page, the general form of the antenna
Array Factor
for an N element array with uniform spacing of d and
phased tapered weights steered towards
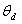 was shown to be: was shown to be:
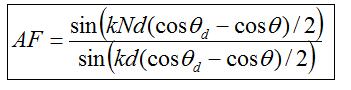 Let's begin by making a variable substitution to simplify the function. We can rewrite the above equation using a variable substitution Q as shown below:
 For N=5, the |AF| (magnitude of the array factor) is plotted in Figure 1 as a function of Qd.
 Figure 1. Magnitude of normalized Array Factor (AF) for N=5. For N=10, the |AF| is plotted in Figure 2.
 Figure 2. Magnitude of normalized AF for N=10.
Figures 1 and 2 indicate that the magnitude of the array factor
becomes more directional with an increasing number of elements, N.
Secondly, the |AF| has a maximum at Qd=0, which occurs when the observation angle
 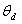 is 0 degrees, then
Qd is physically bounded by to be within the range is 0 degrees, then
Qd is physically bounded by to be within the range

The range of values that are physically realizable are known as the visible region. The
values for Qd that can not occur are in the invisible region.
If d = 0.5wavelengths and the array is steered towards 90 degrees,
then Qd is bounded between -1.57 and 1.57 ( However, if d=0.5 wavelenths and the array is steered towards 0 degrees, then Qd is bounded between 0 and 3.14. In this range, the AF does experience grating lobes within its visible region. Hence, we can conclude that grating lobes may occur for some scan angles and not others. However, if an array is steered towards 0 degrees and does not exhibit grating lobes, then they will also not occur for any other scan angle. Finally, note that if d is increased, the visible region increases in size. Hence, if d is made to be 2 wavelengths, multiple grating lobes will occur within the visible region. If d is made to be 0.25 wavelengths or less, the visible region is greatly reduced in size, and no grating lobes will be seen for any scan angle. Hence, the inter-element spacing strongly controls the AF and whether or not grating lobes appear in uniformly spaced arrays. |
Antenna (Home)
 is equal to the scan angle
is equal to the scan angle
 ). In this
range, the AF does not experience
). In this
range, the AF does not experience