Friis Fórmula Transmisión

Esta página vale la pena leer un par de veces y debe ser entendido en su totalidad. Consideremos dos antenas en el espacio libre (sin obstrucciones en las cercanias) separados por una distancia R: 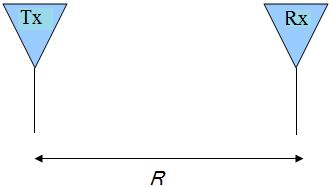Figura 1. Transmisión (Tx) y recepción (Rx) Antenas separadas porR. Supongamos que Vatios de potencia total se entregan a la antena de transmisión. Por el momento, asuma que la antena de transmisión es omnidireccional, sin pérdidas, y que la antena receptora está en el campo lejano de la antena de transmisión. Entonces el poder p de la onda plana que incide en la antena receptora de una distancia R de la antena de transmisión está dada por: Si la antena de transmisión tiene una ganancia en la dirección de la antena de recepción dada por , entonces la ecuación anterior se convierte en el poder: El aumento de los factores de largo plazo en la direccionalidad y las pérdidas de una antena real. Supongamos ahora que la antena receptora tiene una apertura efectiva dada por . Luego, la potencia recibida por la antena () viene dada por: Desde la apertura efectiva de la antena también se puede expresar como: La energía resultante recibido se puede escribir como: Esto se conoce como el Friis transmisión Fórmula . Se refiere el espacio libre de pérdida de trayectoria, ganancias de antena y longitud de onda a la recibir y transmitir las competencias. Este es uno de los fundamentales ecuaciones de la teoría de la antena, y debe tener en cuenta (al igual como la derivación anterior). Por último, si las antenas no son la polarización iguales, el poder por encima recibidas podría se multiplicará por el Polarización Factor de pérdida (PLF) para dar cuenta adecuadamente de este desfase. Véase también decibelios matemáticas.