Frecuencia - Más Conceptos Avanzados

Anterior: La frecuencia básica
Antena básicos Menú
Antena Tutorial de Inicio

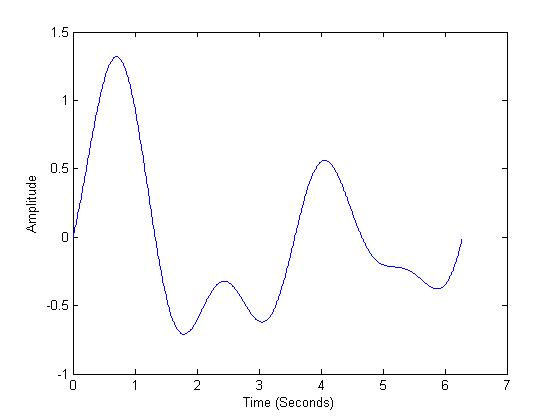
    ¿Por qué es la frecuencia tan fundamental? Para realmente entender que hay que introducir una de las mejores ideas matemáticas cada vez (en serio), y que es "Análisis de Fourier. Tuve una clase sobre Análisis de Fourier en la escuela de posgrado en la Universidad de Stanford, y el profesor se refiere a estos conceptos como "uno de los secretos fundamentales del universo".

Comencemos con una pregunta. ¿Cuál es la frecuencia de la onda de lo siguiente?

a random waveform that represent the fields of an EM wave

Figura 1. Una forma de onda simple.

Bueno, será buscar lo que es el período y darse cuenta de que no es periódica sobre el trazado región. Entonces me decía la pregunta era estúpida. Pero aquí vamos:

Uno de los secretos fundamentales del universo
Todas las formas de onda, no importa lo que garabatear o observamos en el universo, son en realidad la suma de sinusoides simples de diferentes frecuencias.

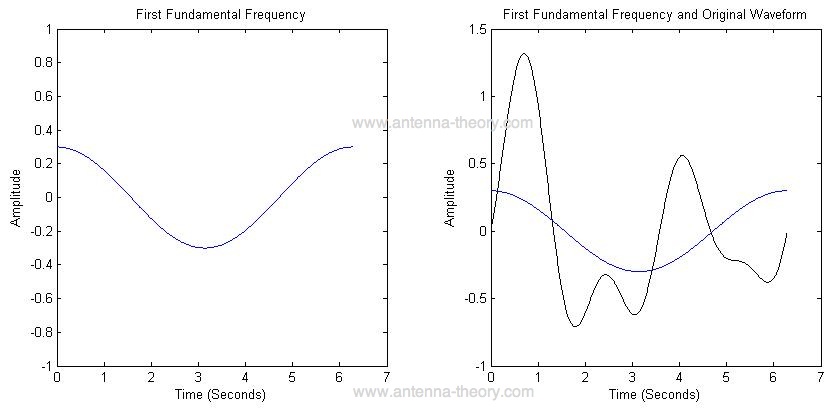
Como ejemplo, vamos a romper la forma de onda en la Figura 1 en "ladrillos" o el de las frecuencias es todo. Esta descomposición se puede hacer con un transformada de Fourier  (O series de Fourier para señales periódicas).

El primer componente es una onda senoidal con periodo T = 6,28 (2 * pi) y la amplitud de 0,3, como se muestra en la Figura 2.

first frequency component of wave

Figura 2. En primer lugar la frecuencia fundamental (izquierda) y forma de onda original (derecha) en comparación.

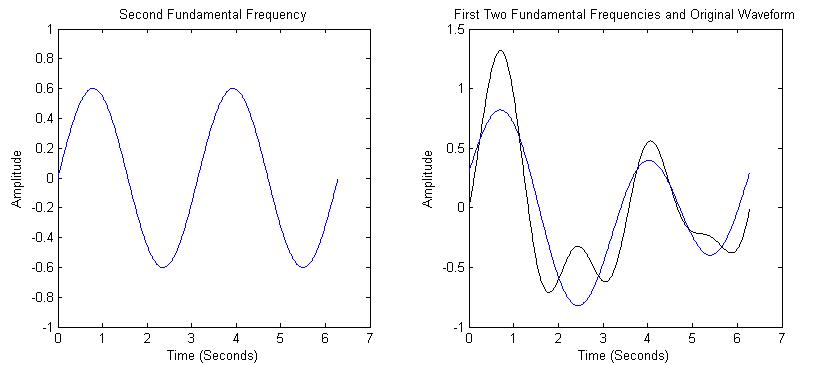
La segunda frecuencia tendrá un periodo medio, siempre y cuando el primero (el doble de la frecuencia). El segundo componente se muestra a la izquierda en la figura 3, junto con la suma de las dos primeras frecuencias en comparación con el forma de onda original.

first and second frequency components of wave

Figura 3. En segundo lugar la frecuencia fundamental (izquierda) y forma de onda original en comparación con los componentes de frecuencia de los dos primeros.

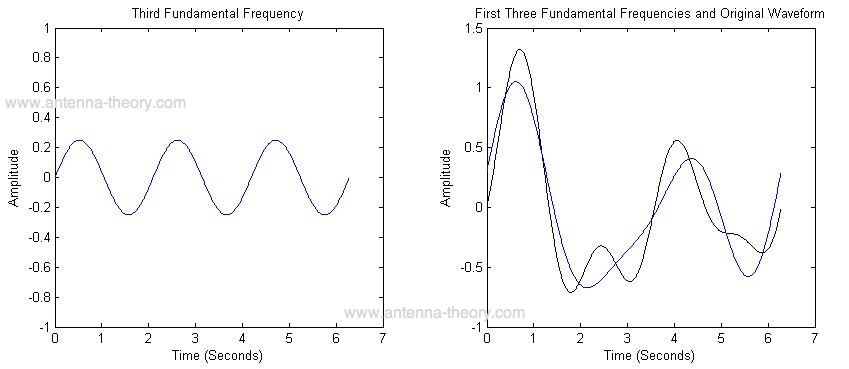
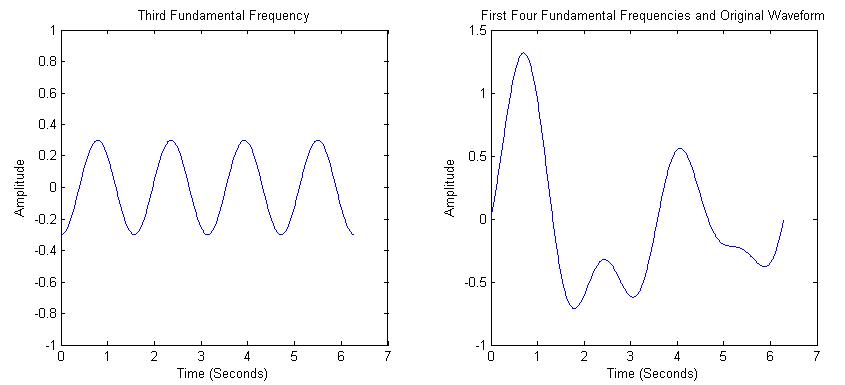
Vemos que la suma de las dos primeras frecuencias está empezando a parecerse a la forma de onda original. La tercera componente de frecuencia es 3 veces la frecuencia como la primera. La suma de los primeros tres componentes se muestran en la Figura 4.

first three frequency components of a wave

Figura 4. Tercera frecuencia fundamental (a la izquierda) y forma de onda original en comparación con los componentes de frecuencia de tres veces.

Por último, la adición del componente de frecuencia en cuarto lugar, tenemos la forma de onda original, que se muestra en la Figura 5.

first 4 frequency components of the wave, producing the original waveform

Figura 5. Cuarta frecuencia fundamental (izquierda) y forma de onda original en comparación con los componentes de frecuencia de los cuatro primeros (se superponen).

Si bien esto parece inventado, es cierto para todas las formas de onda. Esto se aplica a las señales de televisión, señales de teléfonos celulares, las ondas sonoras que viajan al usted habla. En general, las formas de onda no se componen de un número discreto de frecuencias, sino más bien un rango continuo de frecuencias.

A continuación, veremos lo que podemos decir acerca de estos rangos de frecuencia.

Siguiente: Bandas de Frecuencias

Antena básicos Menú

Teoría de Antenas (Inicio)

Antenna Theory (English)