La antena de reflector parabólico (antena parabólica) 2
|
En esta página, vamos a tratar de explicar por qué un paraboloide hace un gran reflector. Para empezar,
que la ecuación de una parábola con la distancia focal F
se puede escribir en el ( x, z ) como avión:
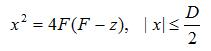 Esto se representa en la Figura 1. 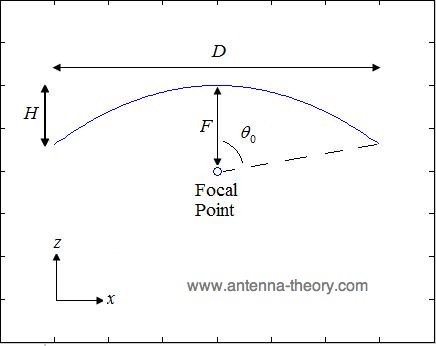 Figura 1. Ilustración de la parábola con la definición de parámetros.
La parábola es completamente descrita por dos parámetros, el diámetro D y la longitud focal F.
También se definen dos parámetros auxiliar, la altura vertical del reflector ( H ) y el máximo
ángulo entre el centro y el borde del plato
(
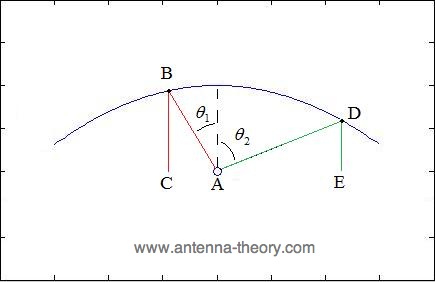 Figura 2. Dos rayos salir del centro de coordinación y reflejada por el reflector parabólico. Hay dos observaciones que pueden hacerse en la Figura 2. La primera es que los rayos acaban viajando en la baja dirección (que se puede determinar por el incidente y reflejada ángulos relativos a la normal de la superficie debe ser igual). Los rayos se dice que son colimado . La segunda observación importante es que la ruta de longitudes de ADE y ABC son iguales. Esto se puede probar con un poco de geometría, que no voy a reproducir aquí. Estos hechos pueden ser probados por cualquier conjunto de ángulos elegido. Por lo tanto, se sigue que:
Como resultado de estas observaciones, se deduce la distribución del campo en el plano focal estará en fase y de viaje en la misma dirección. Esto da lugar a la antena parabólica antenas altamente direccionales diagrama de radiación . Esta es la razón por la forma de la plato parabólico. Por último, al hacer girar la parábola sobre el eje z, se obtiene un paraboloide, como se muestra a continuación.
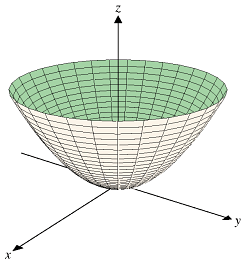 En la siguiente sección, veremos los cálculos de la ganancia de una antena de reflector parabólico.
|
Antenna Theory (Inglés)
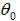 ).
Estos parámetros están relacionados
entre sí por las siguientes ecuaciones:
).
Estos parámetros están relacionados
entre sí por las siguientes ecuaciones: